Integrator I - Untersummen, Obersummen & Integral
Um die
(orientierte) Fläche zwischen dem Graphen von f und der x-Achse zu bestimmen
(geometrischer Ansatz) bzw. um den
Bestand (Änderungseffekt, kumulierte Änderung) bei einer Änderungsfunktion f zu bestimmen (anwendungsorientierter
Ansatz), geht man üblicherweise so vor: Man
approximiert die Funktion f stückweise durch (in der Regel gleich breite)
Treppenfunktionen und rechnet ersatzweise damit. Dabei werden die 'Treppen',
also die stückweise konstante Funktionen, bestmöglich von unten und von oben
angesetzt. So erhält man für n Unterteilungen eine Untersumme Un und eine Obersumme On.
Anschaulich gesprochen: Man ersetzt die krummlinig begrenzte Fläche durch
Rechtecksstreifen bzw. man ersetzt die Änderungsfunktion f durch stückweise
konstante Änderungen. In der Schulpraxis wählt man in der Regel gleich
breite Rechtecksstreifen.
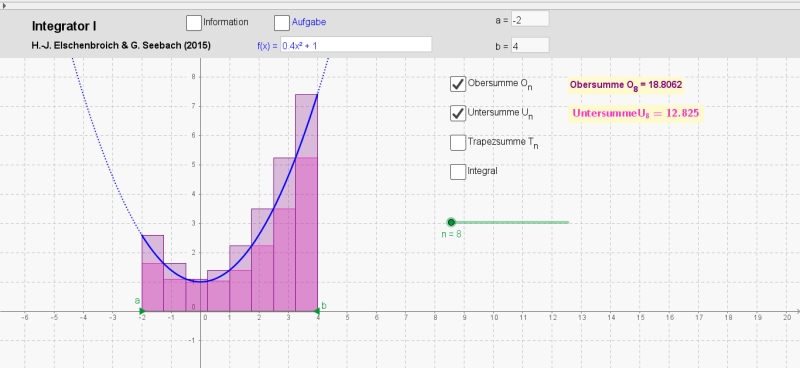
Integrator I für n = 8 mit Untersumme und Obersumme
Vergrößert man n am Schieberegler, so nähern sich Un und On bei schulüblichen, gutartigen Funktionen f immer mehr an und werden im Grenzprozess identisch. Solche Funktionen f heißen dann integrierbar, der gemeinsame Wert ist das Integral von f über [a; b].
Dieses
Vorgehen ist wesentlich für die Entwicklung des Begriffs Integrierbarkeit,
hier ist das 'Einschachteln' von besonderer Bedeutung.
Für die konkrete Berechnung des Wertes ist die Annäherung jedoch relativ schlecht, man braucht
ziemlich große
n, um auf drei oder vier Dezimalstellen zur Übereinstimmung zu kommen. Um
numerisch schneller zu brauchbaren Werten zu kommen, kann man
bei geeigneten Funktionen die
stückweise Annäherung durch konstante Funktionen durch die Annäherung mit
stückweise linearen Funktionen ersetzen. Anschaulich bedeutet dies, dass man
bei der Fläche die Rechteckstreifen duch Trapezstreifen ersetzt. Dieses
Sehnentrapezverfahren ist das einfachste und naheliegendste und zugleich schon
ziemlich effiziente Verfahren zur numerischen Integration. Es gibt weitere,
noch effizientere, aber das soll hier nicht Thema sein.
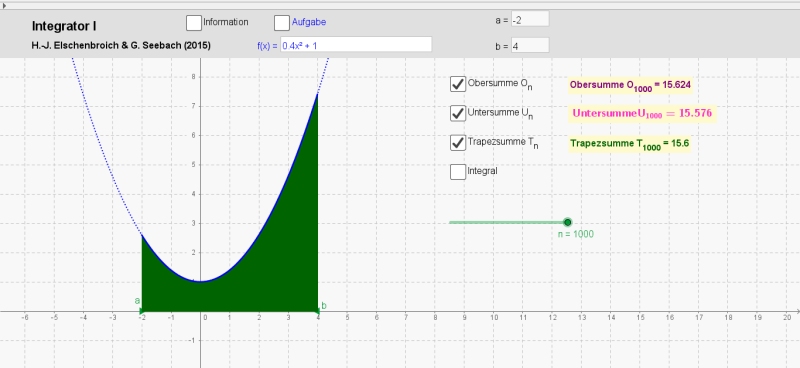
Integrator I für n = 1000 mit Untersumme, Obersumme und Trapezsumme.
Zu
betonen ist, dass beim Integrator I keine komplizierten und trickreichen Zusammenfassungen von Produktsummen
(Rechtecksflächen) mit anschließendem Kürzen erfolgen, sondern dass wir die Software einfach 'straight
forward' rechnen lassen und die Rechenpower der Software ausnutzen. Damit haben wir
jetzt einen auf
der Nutzerebene kalkülfreien Zugang zu den Grundvorstellungen und
Grundaufgaben der Integralrechnung (der vordem ohne digitale Werkzeuge nicht
möglich war), der sich nicht in Termumformungen
verliert, sondern einen direkten Zugang zu den mathematischen Aspekten
und Grundvorstellungen ermöglicht.