Integrator III - Integralfunktion, Integraph und HDI
Beim Verständnis von Integral als Flächeninhalt tritt ein Problem auf, das
beim Verständnis als Bestand, als Änderungseffekt nicht existiert. Haben wir
beim Bestand das natürliche Bild eines Behälters mit Zufluss und Abfluss,
aus dem sich dann der jeweilige aktuelle Bestand ergibt, so müssen wir beim
Flächen-Zugang mit orientierten Flächen arbeiten. Dazu ist es
hilfreich, als Visualisierung die Flächen oberhalb der x-Achse blau zu färben und unterhalb der
x-Achse rot.
Wählt man für einen Punkt Ia mit der x-Koordinate x = x(S) dann als y-Koordinate das entsprechende Integral, so kann man bei Variation von S dann das Verhalten von Ia erkunden und mit Kontrollkästchen die Integralfunktion zeigen lassen. Konzentriert man sich dabei auf das Intervall [a, x], so simulieren wir die Wirkungsweise eines Integraphen. Der komplette Graph der Integralfunktion ist dabei noch leicht gepunktet zu sehen.
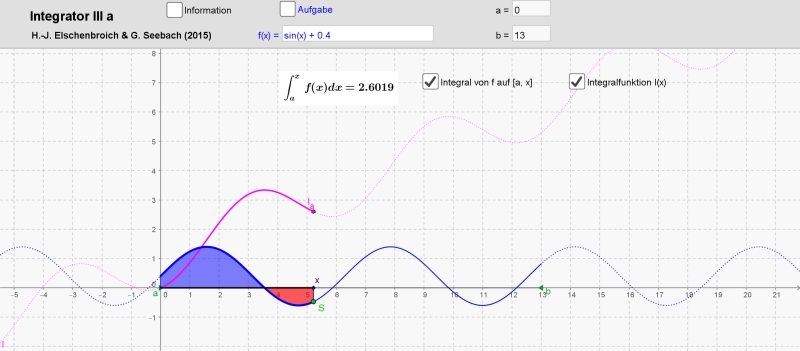
Integrator III a als Integralfunktionszeichner (Integraph)
Am Punkt Ia kann man dann am Graphen der Integralfunktion eine Tangente anlegen. Untersucht man deren Steigung, so stellt man fest, dass diese mit dem Wert von f(x) identisch ist. Das ist die Satzfindung des Hauptsatzes der Differenzial- und Integralrechnung!
Als netten graphischen Effekt und visuelle Unterstützung kann man noch am Punkt Ia einen stilisierten Lenker mit Lampe einblenden, der auf dem Graphen der Integralfunktion zu fahren scheint.
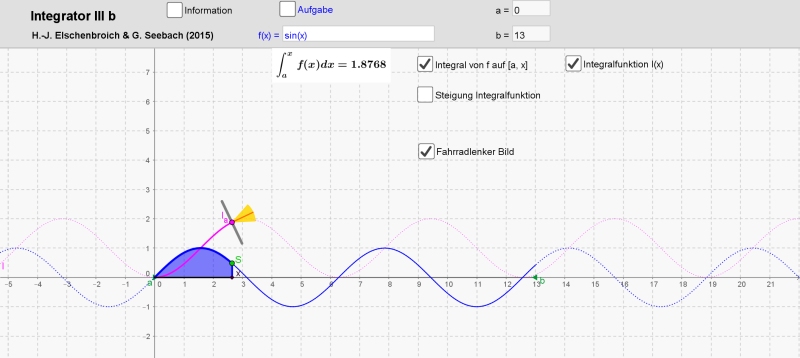
Integrator III b und Haupsatz-Findung
Naturgemäß startet hier die Integralfunktion I an der Stelle a immer mit dem Wert 0. Will man in Anwendungsbeispielen zum Startzeitpunkt mit einem anderen Startwert c beginnen, so kann man im Integrator III c einen Wert für c eingeben.
Wir haben hier mit der Befehl Integralfunktion aus dem CAS-Fenster von GeoGebra gearbeitet. Man kann aber auch rein graphisch mit Ortslinien vorgehen (ist deutlich zeitintensiver), siehe Integrator III d. Eine Stärke dieses graphischen Ansatzes besteht darin, dass er auch bei Funktionen wie f(x) = 3 sin(0.01 x²) durchführbar ist, von denen man weiß, dass sie wegen der Stetigkeit nach dem Hauptsatz eine Stammfunktion/ Integralfunktion haben, man diese aber nicht in geschlossener Form vermittels der gängigen Integrationsregeln als Term angeben kann. Mit einem Integraphen kann man aber den Graphen zeichnen!
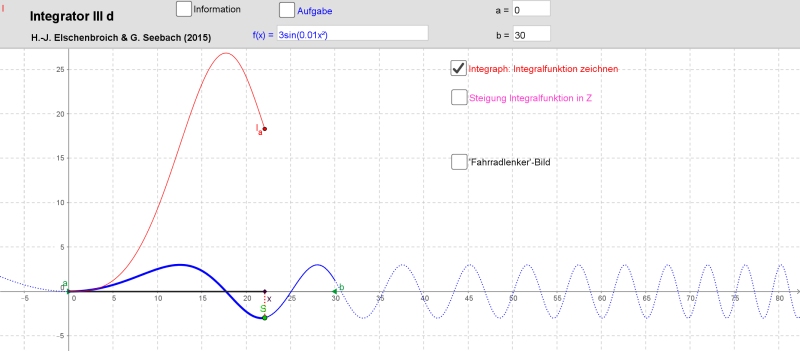
Integraph
bei einer Funktion, die man nicht mittels HDI integrieren kann.