Integrator IV - Stammfunktionszeichner
Blum (1982) weist darauf hin, dass ein Integraph der
Verwendung nach ein Integralfunktionszeichner ist (Integrator III), demWesen nach
aber ein Stammfunktionszeichner.
Will man nun zu gegebenem f eine Stammfunktion zeichnen, so bietet sich hier ein näherungsweises, punktweises Vorgehen an. Dazu nutzt man eine Schrittweite h, die man über einen Schieberegler n erhält mit h = (b-a)/n. Beim Stammfunktionsgraphen geht man dann an der Stelle x um h in x-Richtung nach rechts und um h·f(x) in y-Richtung nach oben/unten. Damit bekommt man einzelne Graphen-Punkte einer Näherung der Stammfunktion F. Dies ist letztlich das Polygonzug-Verfahren von Euler-Cauchy zur näherungsweisen Lösung von Differenzialgleichungen. Man erhält für immer kleinere Schrittweiten h immer bessere Näherungen der Stammfunktion F. Aus optischen Gründen kann man dann diese Punkte noch mit einem Streckenzug verbinden.
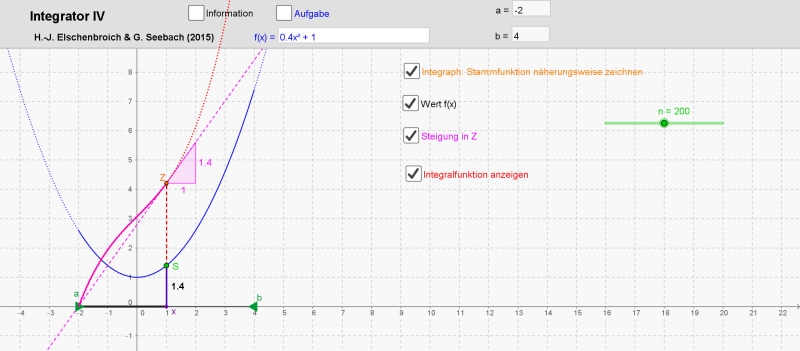
Vergleicht
man den so konstruierten Graphen der Näherung von F für genügend große n mit dem Graphen
der Integralfunktion, so stellt man fest, dass die Abweichung zunehmend
kleiner wird und schließlich anschaulich nicht mehr erkennbar ist.
Auch dies
führt uns wieder zur Aussage des Hauptsatzes.
Dieser
Weg ist aber deutlich anspruchsvoller und auch nicht gerade selbsterklärend.