Integrator V - Rotationskörper
Ein Rotationskörper ensteht, wenn der Graph einer Randfunktion
f um die x-Achse rotiert (auf eine Rotation um die y-Achse gehen wir hier
nicht ein). Will man das Volumen berechnen, so kann man
auf die Idee der Integrierbarkeit zurückgehen und die Untersummen- und Obersummen-Rechtecke
mit rotieren lassen. So werden aus den Rechtecken dann zylindrische
'Scheiben'.
Diese 'zu Fuß' zu berechnen und die Produktsummen umzuformen, wird meist als zu lästig angesehen. Deshalb geht man schnell zur Integration der Ersatzfunktion g(x) = p f2 (x) über und es werden entsprechende Integrationsregeln angewandt. Leider geht das oft auf Kosten des Verstehens. Mit dynamischer Mathematik-Software wird es nun möglich, diese Berechnungen direkt mit der Funktion f durchzuführen und das auch in 3D zu visualisieren. Die 3D-Ansicht kann durch einfaches Ziehen passend gestalten.
Die Rechenarbeit wird wieder der Software übertragen. So
versteht und sieht man jetzt direkt, worum es geht.
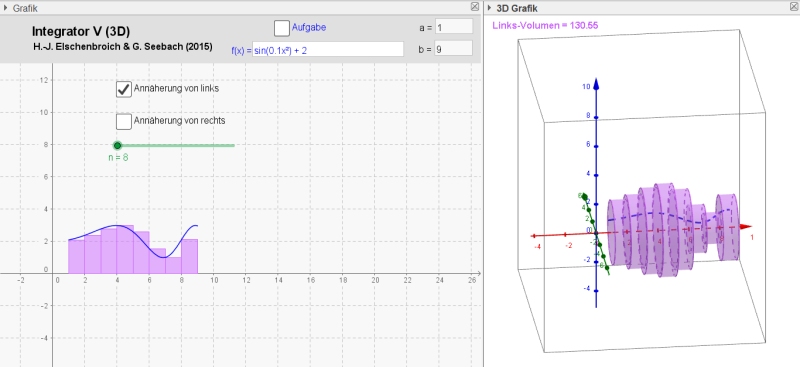
Rotation
von f(x) = sin(0.1·x²) +2 auf [1; 9] mit n = 8
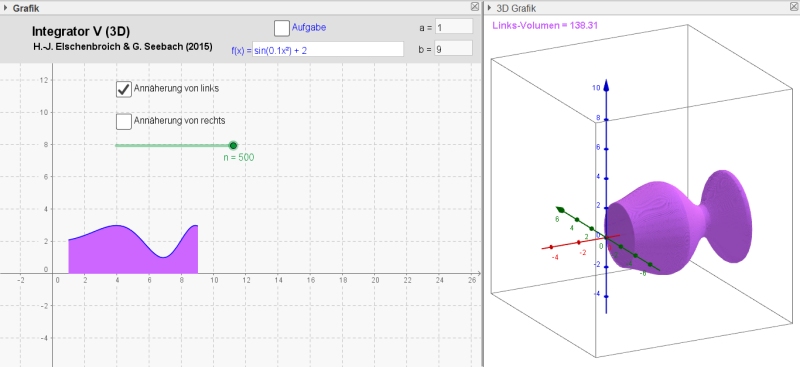
Rotation
von f(x) = sin(0.1·x²) +2 auf [1; 9] mit n = 500
Aus softwaretechnischen Gründen wurde hier in der Umsetzung nicht mit Unter- und Obersummen gearbeitet, sondern mit Links- und Rechtssummen (was ja bei integrierbaren Funktionen f auf dasselbe hinausläuft).
Für große n bekommt man eine relativ 'glatte' Oberfläche, die Berechnung ist dann aber einigermaßen zeitaufwändig. Mit dem GeoGebra-Befehl Oberfläche kann man stattdessen die glatte Oberfläche direkt, effizient und gut aussehend erzeugen.
Dies
bietet dann die Möglichkeit, auch eine zur x-Achse senkrechte Fläche durch
den Körper wandern zu lassen und die kreisförmigen Querschnittsflächen zu
betrachten. Für die Querschnitte erhält man die Funktion qu(x) =
p
f²(x).
Dies gibt einen
Perspektivwechsel: Statt der Rotation der Fläche unter dem Graphen von f um
die x-Achse kann man sich den Körper jetzt durch die Bewegung einer
(Kreis-)Fläche längs der x-Achse entstanden denken. Das Volumen ist dann das Integral von qu(x)
über [a, b].
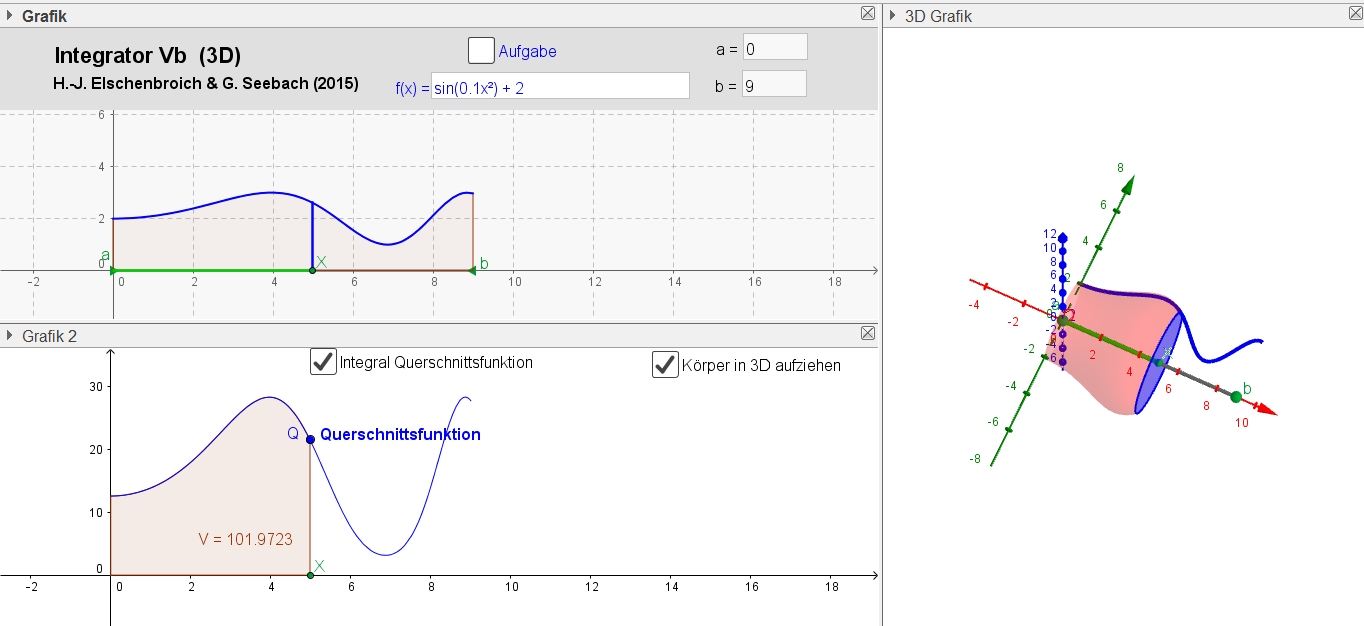
Volumen und Querschnittsflächen
Dieser
Ansatz der Bewegung einer Querschnittsfläche ist am Rande bemerkt
leistungsfähiger als die Rotation um die x-Achse. Denn man kann in gleicher
Weise auch nicht-kreisrunde Querschnittsflächen betrachten (z.B. bei einer
quadratischen Pyramide)!